두 벡터가 A = (3, 2), B = (4, 1) 일때 벡터 B에 대한 벡터 A의 투영 벡터를 구해보자!!
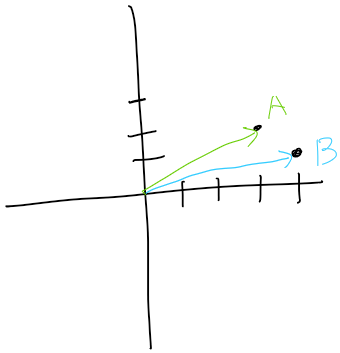
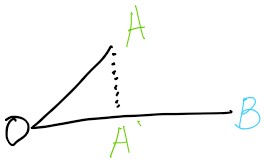
A의 투영벡터는 A'임 즉 A'를 구하면 됨
우선 A'의 길이는 cosθ = A'(밑변) / A(빗변) 이기 때문에
A'의 길이는 = cosθ * A의 길이 라는걸 알 수 있음
그렇다면 A' 의 벡터는 어떻게 구하면 될까!!?
간단함!
A의 길이 * cosθ * [B의 단위벡터] 를 곱하면 됨
1. A의 길이
킹타고라스의 정리를 이용하면 됨 √(3² + 2²) = √13 이 A의 길이가 됨
2. B의 단위벡터
단위벡터는 킹타고라스의 정의로 B의 길이를 구한 후 벡터B에 나눠주면됨
즉 B의 단위벡터 = ( 4/√17, 1/√17 )
지금 까지 계산해서 나온 값들을 바탕으로 다시 식을 써보자면
A'의 벡터 = √13 * ( 4/√17, 1/√17 ) * cosθ 임
3. cosθ
이것만 구하면 끝남!
그럼 이건 어떻게 구하는가..
내적 구하는 식을 이용하면 됨!
A 와 B의 내적을 구하는 식은 2개가 있음
1. 벡터A * 벡터B
(3, 2) * (4, 1) = (12, 2) 이후 두 값을 더해주면됨
즉 A와 B의 내적은 14임
2. 내적 = A의 길이 * B의 길이 * cosθ
이렇게 두가지의 방법이 있는데
우리는 벡터의 정확한 값을 알고 있으므로 1번째 방법으로 이미 내적을 구했음
킹렇다면 이 내적의 값과 두번째 식을 이용해서 cosθ의 값을 알아낼 수 있지 않을까!!?
14 = A의 길이 * B의 길이 * cosθ
즉!
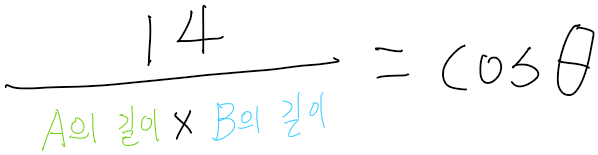
이걸 위의 A'의 벡터를 구하는 식 [A의 길이 * [B의 단위벡터] * cosθ] 에 넣어보면
A'의 벡터는
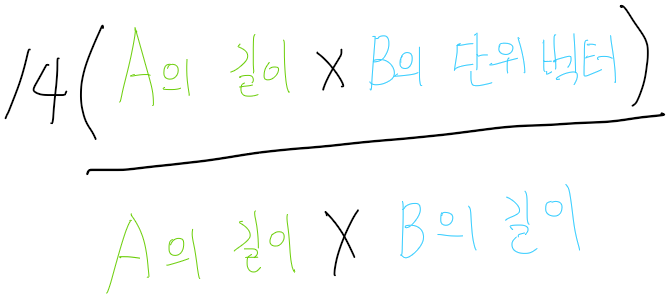
=
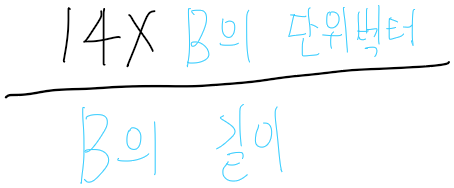
=
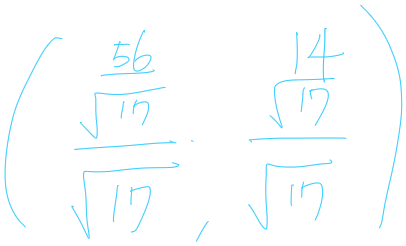
=
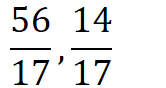
이렇게 투영 벡터를 구할 수 있음
LIST