A좌표계의 P벡터를
B좌표계의 좌표로 변환 시키는 행렬
좌표계 변환 행렬
- 벡터의 변환

A좌표계에서 P의 위치는
x * (X축 단위벡터) + y * (Y축 단위벡터)

그렇다면 너무나 당연하게도
B좌표계에서 P의 위치는
x * (A좌표계의 X축 단위벡터를 상대적으로 표현한 단위벡터) +
y * (A좌표계의 Y축 단위벡터를 상대적으로 표현한 단위벡터)

즉 B좌표계에서의 X,Y축 단위벡터를 이용하면 간단하게 변환이 된다는것을 알 수 있음
이것을 3차원으로 일반화 하면

- 점의 변환
점에 대한 좌표 변경은 벡터와 아주 약간 다름

A 좌표계의 점 P는

위 처럼 표현할 수 있는데 여기서 Q는 A의 원점을 뜻함
즉 벡터의 변환과 달리 점의 좌표계 변환은 좌표계의 원점을 추가로 더해줘야 함
그렇다면
B 좌표계의 점 P는

이를 3차원으로 일반화 하여

일때

라고 표현할 수 있음
여기서 QB는 좌표계 A의 원점을 좌표계 B에 상대적으로 표현한 점임
행렬 표현
벡터와 점에 대한 좌표 변경 변환 공식을 정리하자면 다음과 같음!
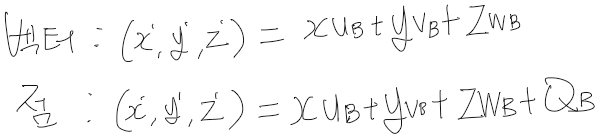
동차좌표를 사용한다면 벡터와 점을 다음과 같은 하나의 공식으로 처리할 수 있음

좌표계의 원점을 포함하지 않는 벡터의 경우 W에 0을 넣어주면 되고
점의 경우 1을 넣어주면 됨
위의 공식을 행렬로 표현해보자면
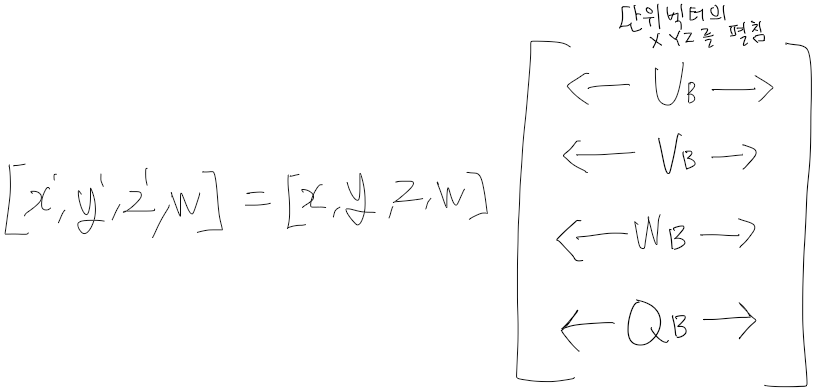
즉

이렇게 펼칠 수 있는거임
위의 (Ux, Uy, Uz), (Vx, Vy, Vz), (Wx, Wy, Wz), (Qx, Qy, Qz)는
좌표계 A의 원점과 축들을 좌표계 B에 상대적인 동차좌표로 표현한 것임
국소 공간(local space)에서 물체를 정의하고 세계 공간(world space)에서 그 물체를 사용할 때
위의 공식만 사용하면 아주 간단하게 국소 좌표계의 물체를 세계 좌표계에 옮길 수 있게 되는거
'공부 > 수학' 카테고리의 다른 글
| 게임에서의 내적과 외적의 활용 (0) | 2025.03.04 |
|---|---|
| 변환 행렬 (SRT) (1) | 2022.12.01 |
| 행렬 기초 (0) | 2022.08.28 |
| 투영 벡터 구하기 (0) | 2022.08.26 |
| 벡터의 내적 (0) | 2022.08.23 |