벡터의 내적은 그 결과가 벡터가 아닌 스칼라가 되는 벡터의 곱셈임
내적 | 內積 | inner product
적은 '곱한다'는 뜻이다. 벡터의 곱하기는 두 가지 정의가 있는데, 내적은 벡터를 마치 수처럼 곱하는 개념이다.
벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱한다. 예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱한다. 두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은 0이다. 내적은 한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다. --- https://wikidocs.net/22384
내적 계산법
-

선분 OA 를 선분 a, OB를 선분 b라고 정의할때 벡터의 내적은 a • b가 됨!
참고로 곱하기 표현은 외적의 경우 X로 내적은 • 로 표현함
a • b 는 아래의 수식으로 값을 알아낼 수 있음

3차원 벡터의 내적
두개의 3차원 벡터의 경우 이렇게 표현이 됨
U = (Ux, Uy, Uz), V = (Vx, Vy, Vz) 일때
U • V = UxVx + UyVy + UzVz
U • V = ||U|| ||V|| cosθ
u = 1, 2, 3, v = -4, 0, -1
u * v = -4, 0, -3 = -7
||U|| 는 U벡터의 크기(길이)를 뜻함
||U|| 구하는 법

빗변의 길이가 a인 삼각형을 보면 피타고라스의 정리에 따르면
a =

라는걸 알 수 있음
이제 밑변이 a이고 높이가 y인 삼각형을 이용해 ||U||의 크기를 구해보자면
||U|| =
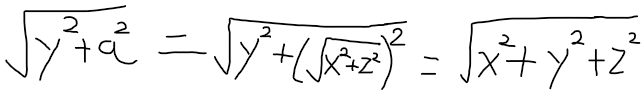
이렇게 됨
예제 1) 두 벡터의 내적을 구하시오
u = 1, 2, 3
v = -4, 0, -1
u * v = -4, 0, -3 = -7






예제 2) 두 벡터의 내적을 구하시오
u = 3, 4, 2
v = 1, -5, 2
uv = 3, -20, 4 = -13
||u|| = √9+ 16 + 4 = √29
||v|| = √1 + 25 + 4 = √29
uv = ||u|| * ||v|| * cos
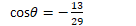
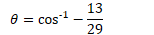
참고
https://www.youtube.com/watch?v=IOf1o72aKDc&t=196s
,DirectX 12를 이용한 3D 게임 프로그래밍 입문 (한빛미디어)