SRT는 Scale, Rotation, Translation의 약자로
DX에서의 SRT는 크기와, 회전, 이동을 뜻함
- Translation
(x, y, z)의 좌표가 있을때 이 좌표를
x축으로 1만큼 이동하고 싶다 라고 할때는
너무나 당연하게도 x+1을 해주면 됨
이게 바로 Translation 변환 행렬의 개념이라고 볼 수 있음
(x,y,z)를 넣어서 (x+1,y,z)가 나오게 하려면 간단하다!
행렬의 곱이 어떤식으로 동작하는지만 생각해 보면 되는데
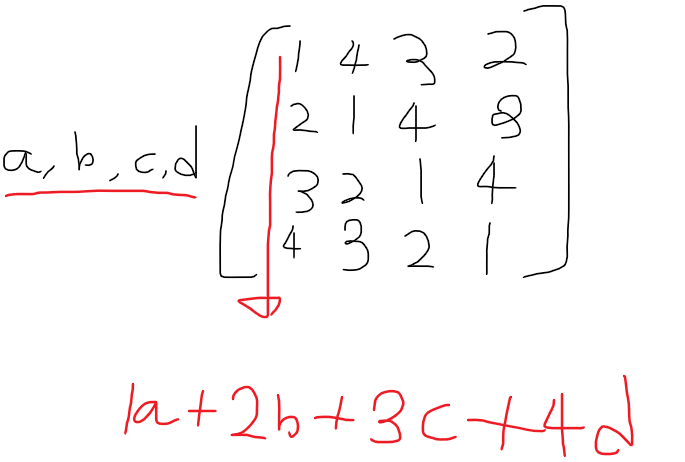
w라는 가상의 원소를 넣어두고 (x,y,z,w)
벡터에 더해주고 싶은 값을
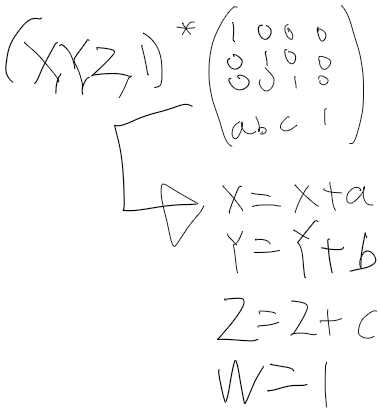
abc에 넣어준다면
Translation 변환 행렬 완성
- Scale
scale은 그냥 곱해주면 되는거기 때문에
translation보다 쉬움!
scale이 2배 더 커지게 하고싶다?
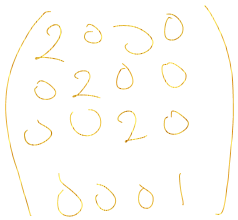
끝!
-Rotation
X =
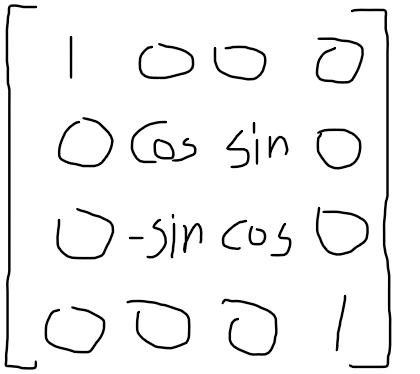
Y =
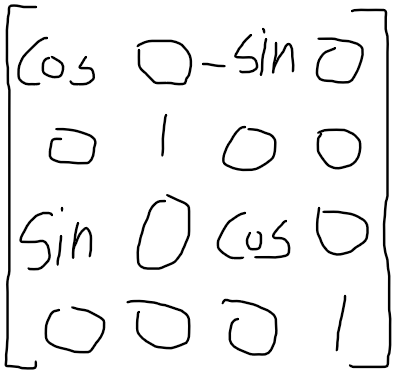
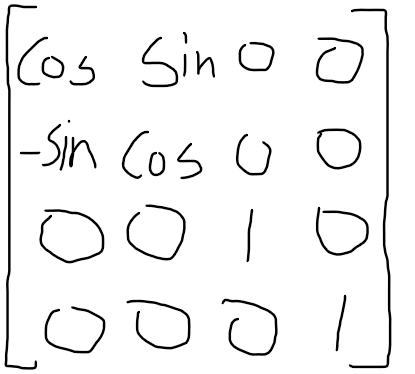
Z =
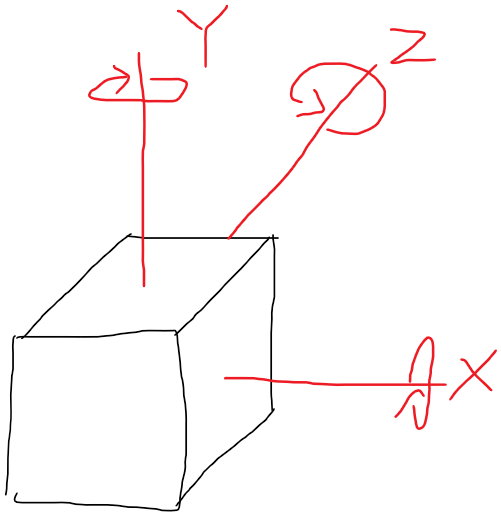
삼각비
Sin 빗변과 높이의 길이의 비 기준각이 A일때 sinA = 높이 / 빗변 Cos 빗변과 밑변의 길이의 비 기준각이 A일때 cosA = 밑변/빗변 Tan 밑변과 높이의 길이의 비 기준각이 A일때 tanA = 높이 / 밑변 sin30 = 높
flrjtwjrjt.tistory.com
행렬 기초
행렬의 기본 용어 행별 : 수나 문자를 직사각형 형태로 나타낸 것. https://www.youtube.com/watch?v=E7f1V92y7Fg&list=PLxz77rwoJPpWMrEaUpfGTG9P7X_faMYGi
flrjtwjrjt.tistory.com
Z축 증명
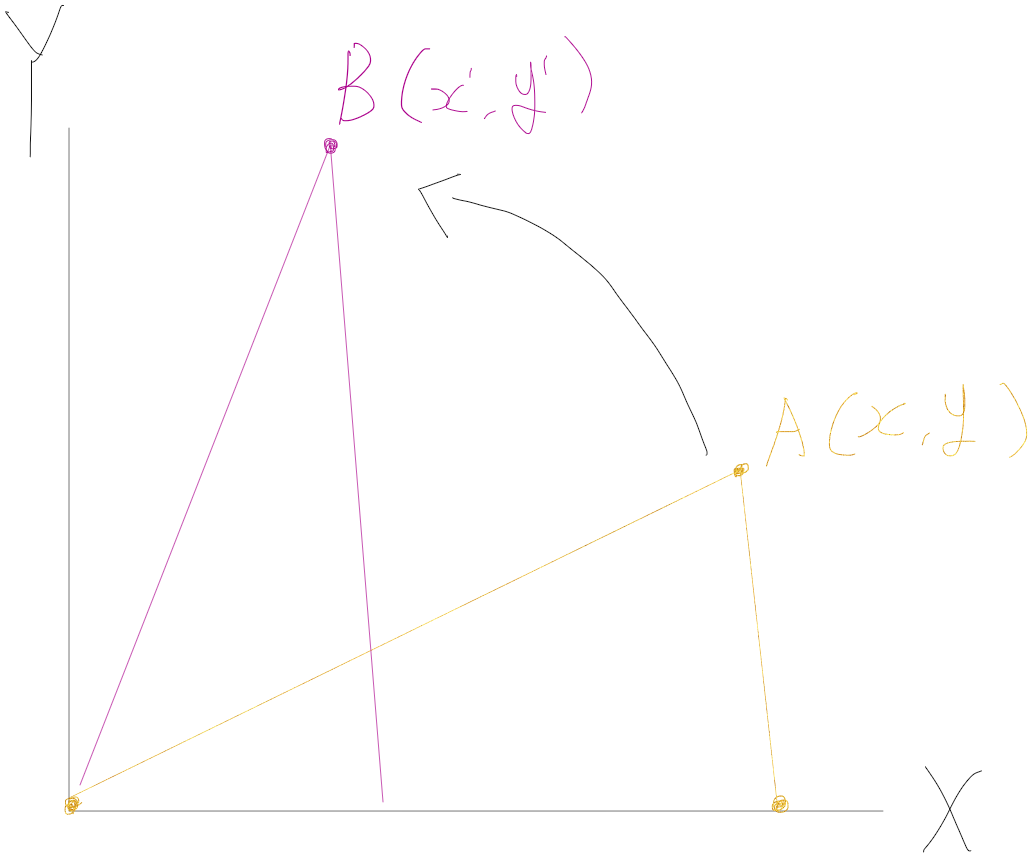
X,Y축을 가지고 있는 평면 좌표계에서 A점이 B로 회전한다고 했을 때
이건 Z축의 회전이라고 할 수 있음

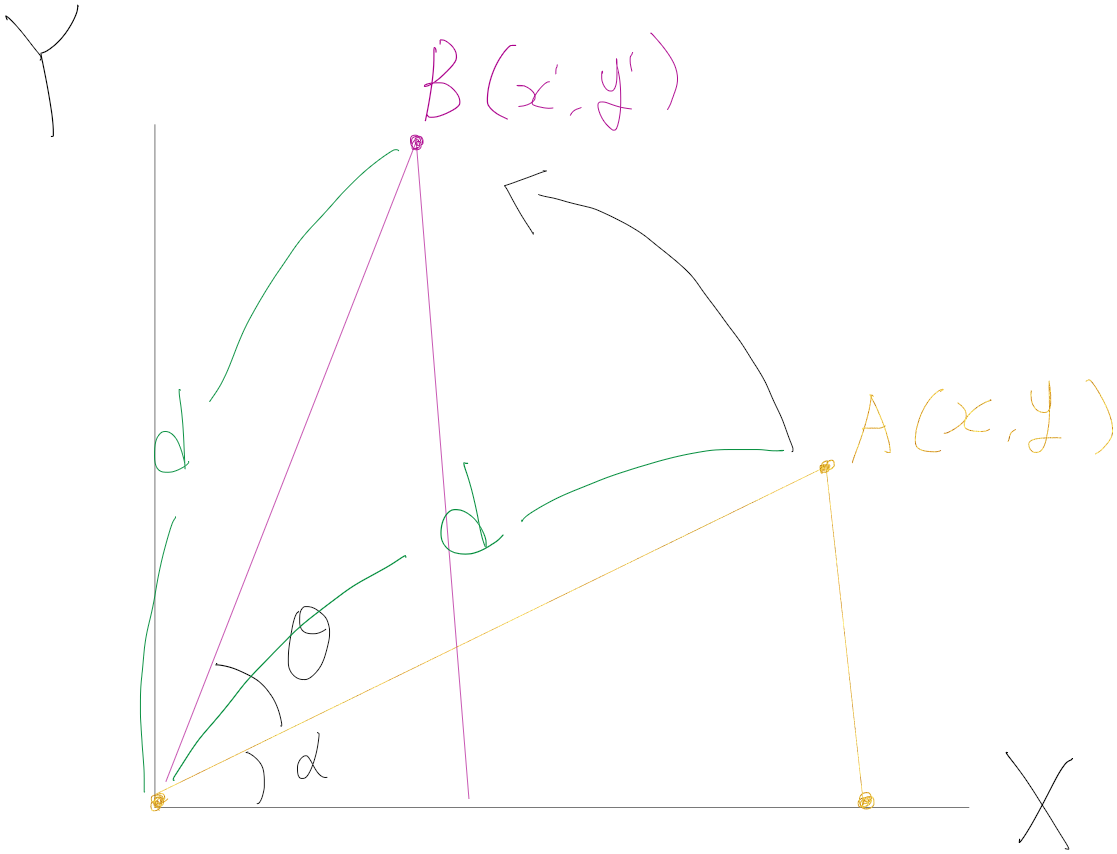
각 좌표의 대각 길이를 d라고 할때
삼각비를 통해 밑변과 높이를 구해보면
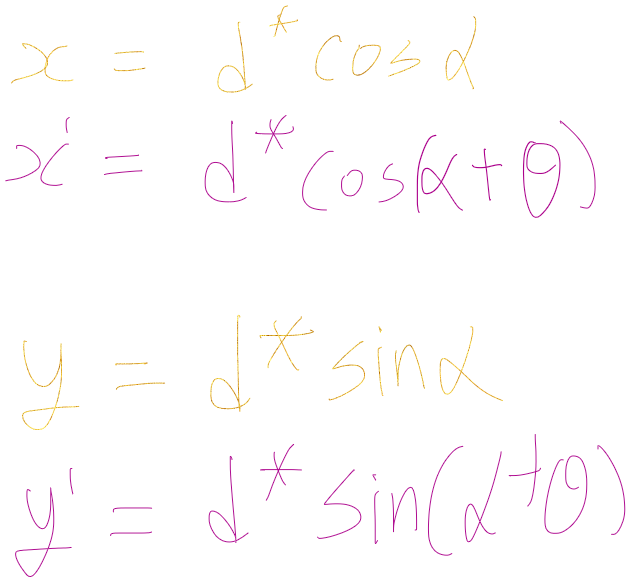
이처럼 회전된 좌표의 x,y값을 쉽게 알아낼 수 있음
이때 삼각함수의 덧셈 정리 코코싸싸랑 싸코코싸로 정리를 해주면
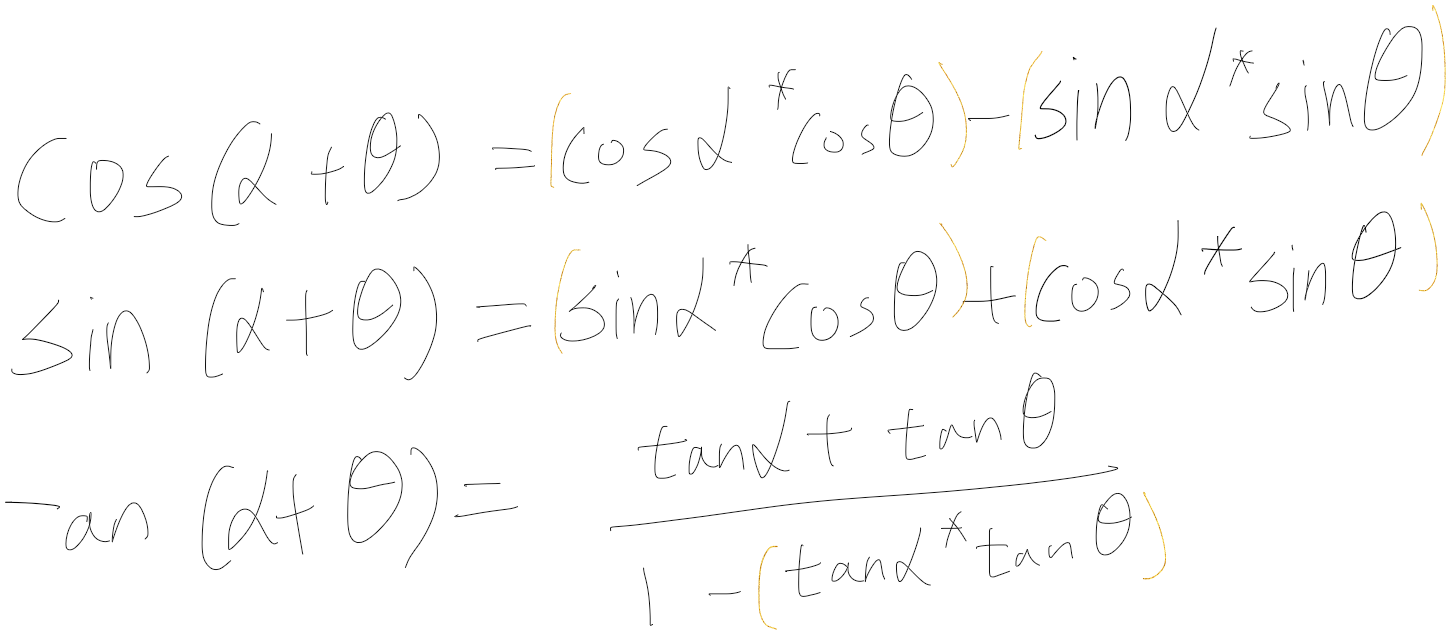
덧셈정리
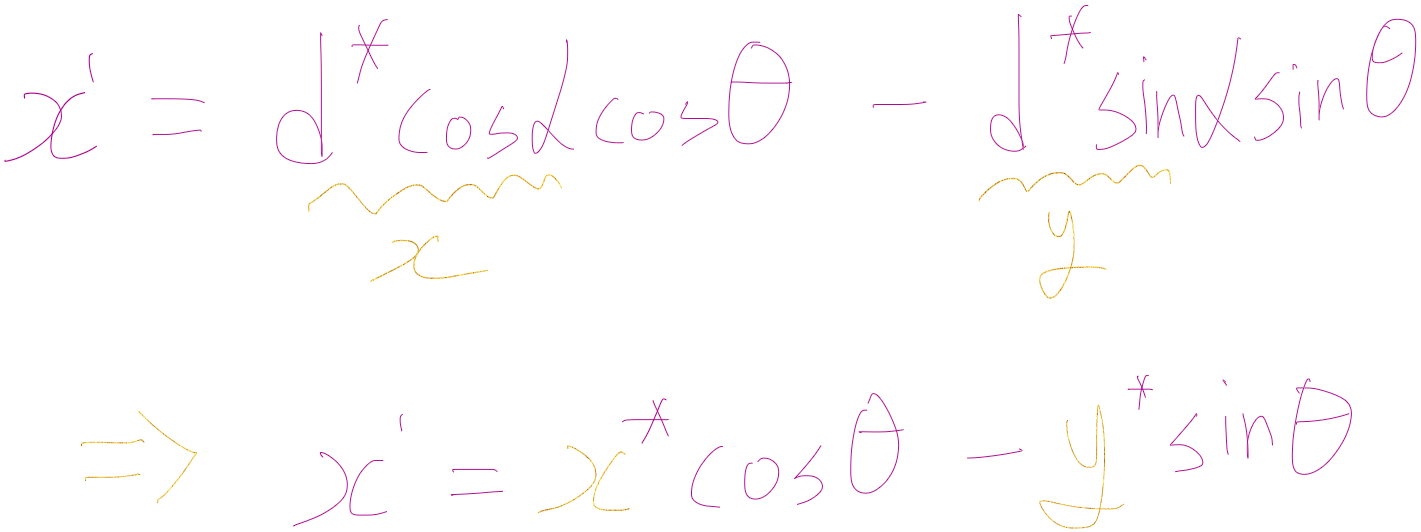
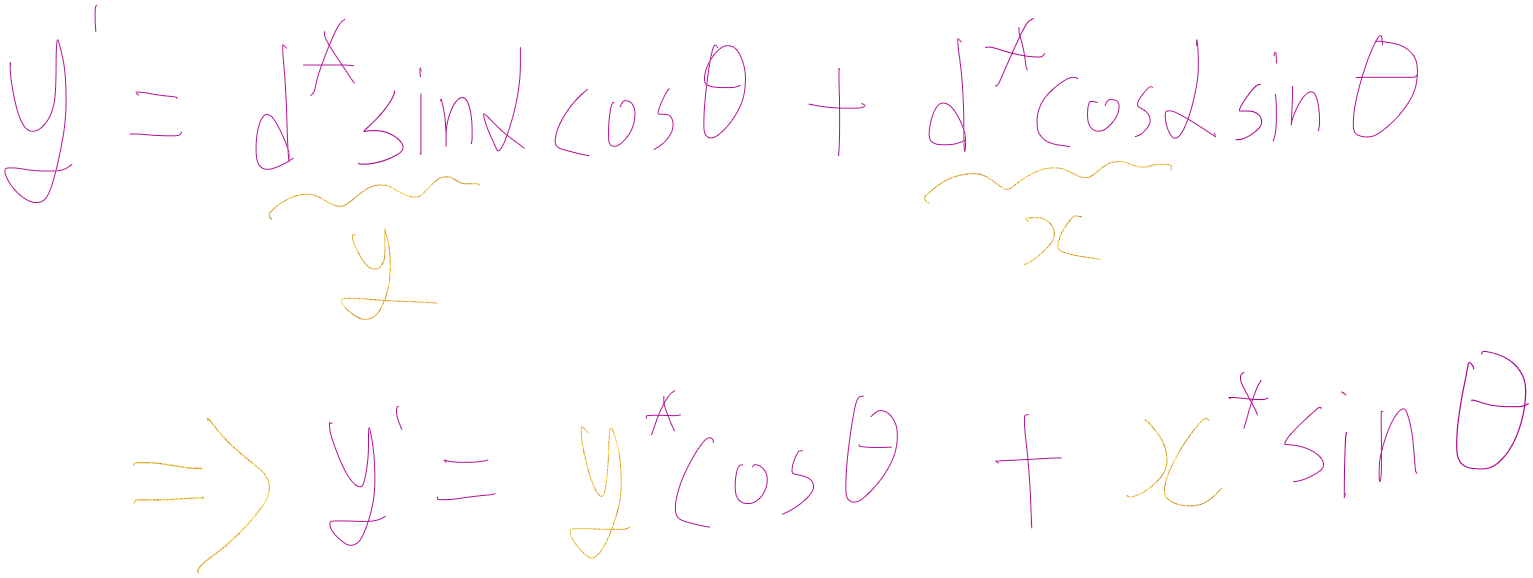
이런식으로 정리가 되는 것을 알 수 있는데
위에서 미리 보여준 Z축 행렬로 다시한번 증명을 해보면
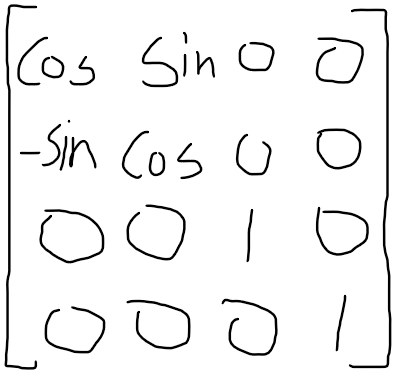
x,y,z,1을 넣는다고 했을때
x = xCos - ySin
y = xSin + yCos
딱! 맞는 것을 알 수 있음!
X랑 Y도 그냥 똑같기 때문에 따로 정리는 안함!