네트워크 플로우 알고리즘
한 정점에서 다른 정점으로 데이터가 흐를때 각각의 간선으로 보낼 수 있는
데이터 용량을 지키면서 목표 정점까지 최대로 보낼 수 있는 데이터의 양을 구하는 알고리즘
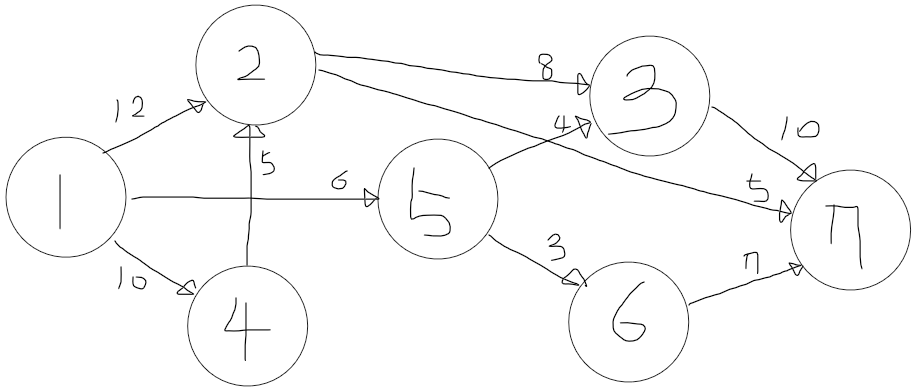
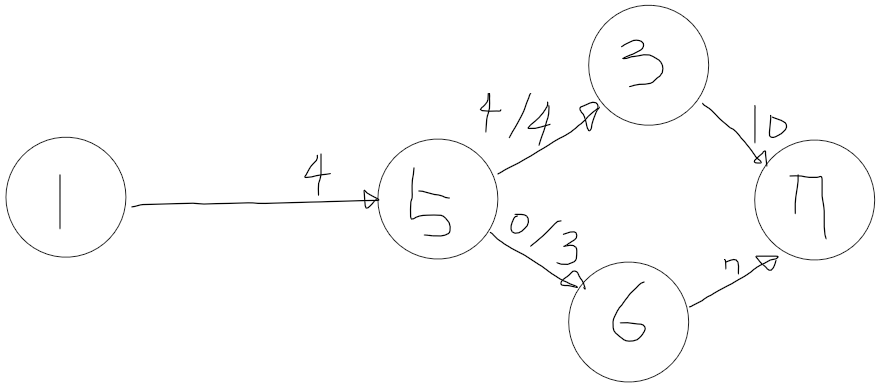
위의 그래프를 보고 1번 노드에서 7번 노드로 데이터를 보낼때
최대 얼마나 보낼 수 있을까?
위 그래프는 방향그래프이기 때문에
계산을 할때 보통 간선의 방향만 보면서 계산을 하게 됩니다.
따라서 아래와 같이 생각해볼 수 있습니다.
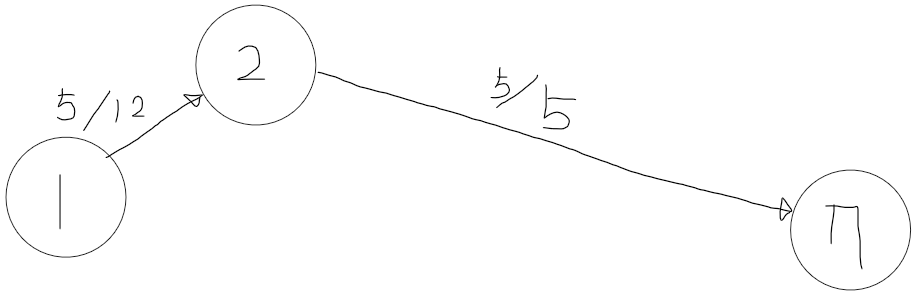
1 -> 2 -> 7 은 5만큼 보낼 수 있고
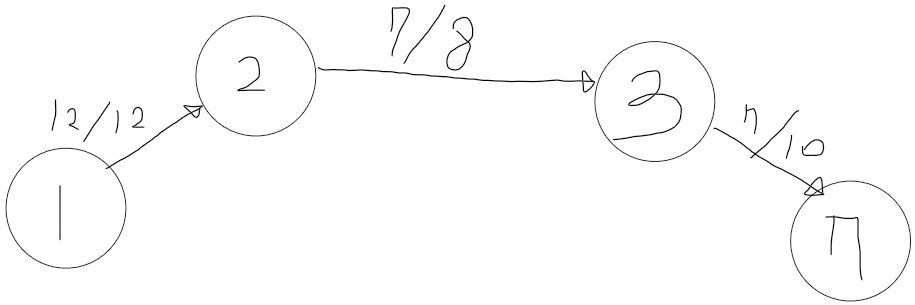
1 -> 2 -> 3 -> 7은 7만큼 보낼 수 있고
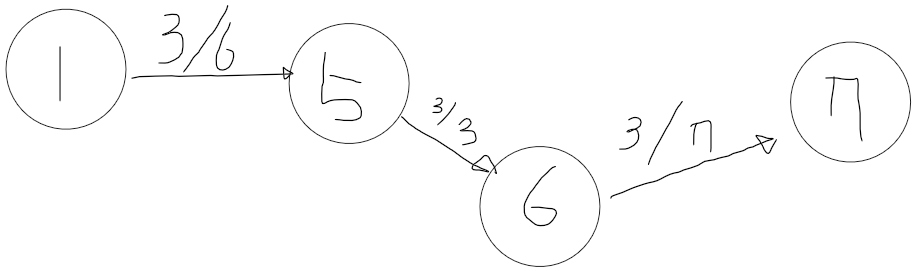
1 -> 5 -> 6 -> 7은 3만큼 보낼 수 있고
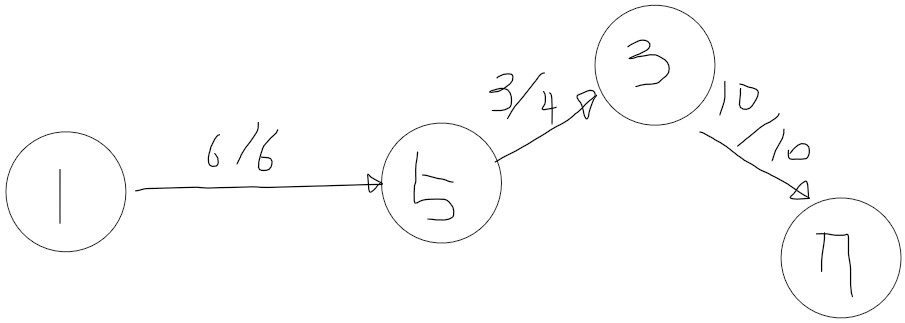
1 -> 5 -> 3 -> 7도 3만큼 보낼 수 있고
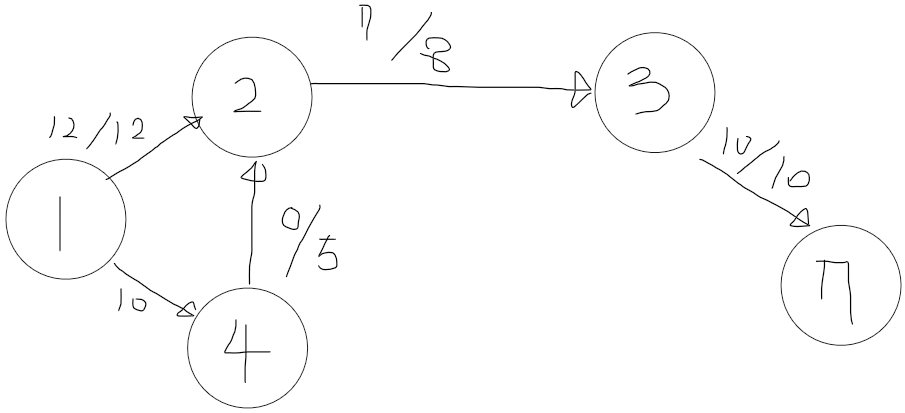
1 -> 4 -> 2 - > 3 - > 7 로 0만큼 보낼 수 있게됩니다
-----그렇다면 최대로 보낼 수 있는 데이터는 18??
그런데 위의 경로 말고는 다른 방법이 없을까?
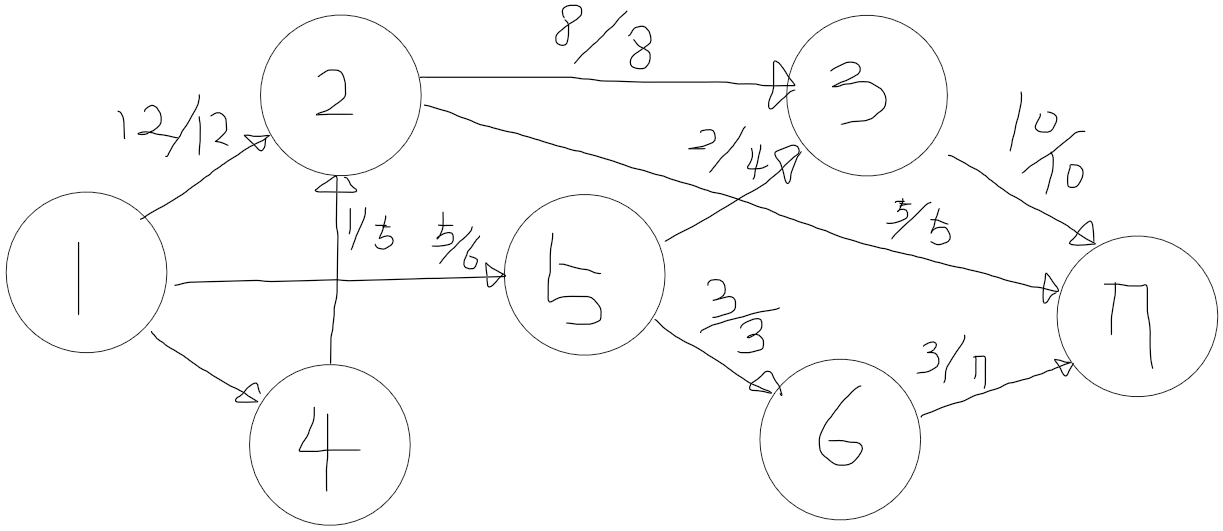
위와 같은 방식으로도 18만큼의 데이터를 전달 할 수 있습니다.
이렇듯 18만큼의 데이터를 흐르게하는 방법은 여러가지가 있습니다.
그렇다면 이런 모든 경로에 대한 탐색 및 비교가 가능한 알고리즘이 있어야하지 않을까??
그렇다면 어떻게 문제를 해결해야할까?
아래와 같은 임의의 간선들을 추가해주는 것만으로 효과적으로 문제를 해결할 수 있습니다.
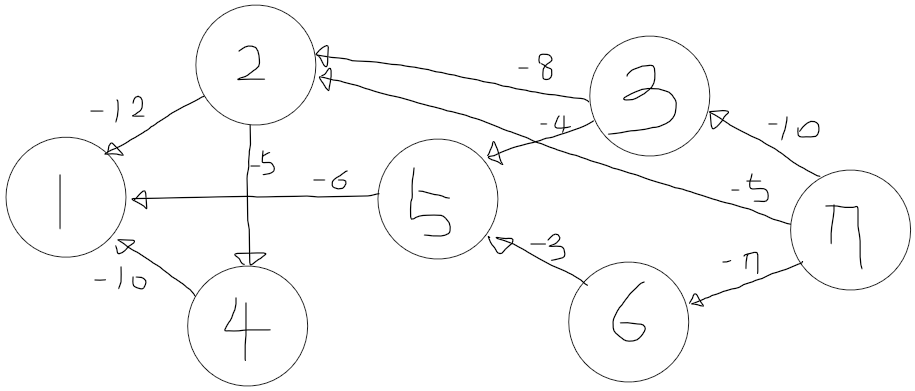
위 처럼 간선이 음수로도 흐른다고 생각해 보면
이미 흐르고 있는 데이터도
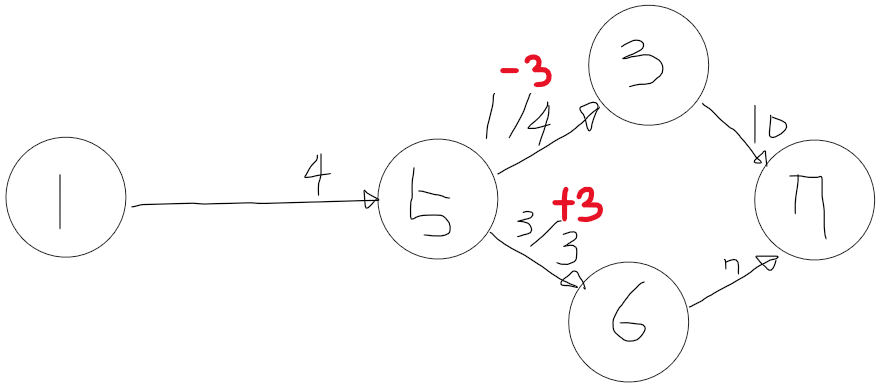
이런식으로 경로를 트는것이 가능해집니다.
이렇게 되면 더 효율적으로 모든 경로에 대한 탐색 및 비교가 가능해지게 됩니다.
#define MAX 100
int limit[MAX][MAX];
int flow[MAX][MAX];
int parent[MAX];
vector<int> v[MAX];최대로 흘려보낼수 있는 양을 나타내는 limit,
흘려 보내고 있는 데이터의 양을 나타내는 flow,
현재노드로 오기 전의 부모 노드를 찾아주는 parent배열을 만들어 줍니다.
그래프를 나타내는 vector도 생성해줍니다.
int main()
{
v[1].push_back(2);
v[2].push_back(1);
cost[1][2] = 12;
v[1].push_back(4);
v[4].push_back(1);
cost[1][4] = 10;
v[1].push_back(5);
v[5].push_back(1);
cost[1][5] = 6;
v[2].push_back(3);
v[3].push_back(2);
cost[2][3] = 8;
v[2].push_back(7);
v[7].push_back(2);
cost[2][7] = 5;
v[3].push_back(7);
v[7].push_back(3);
cost[3][7] = 10;
v[4].push_back(2);
v[2].push_back(4);
cost[4][2] = 5;
v[5].push_back(3);
v[3].push_back(5);
cost[5][3] = 4;
v[5].push_back(6);
v[6].push_back(5);
cost[5][6] = 3;
v[6].push_back(7);
v[7].push_back(6);
cost[6][7] = 7;
cout << MaxFlow(1, 6) << endl;
}그래프를 구성하는 간선과 그 간선을 뒤집어서 vector에 넣어줍니다.
시작 위치와 끝 지점 위치를 지정해주고 함수를 실행합니다.
int MaxFlow(int start, int end)
{
int result = 0; // end로 보낼 수 있는 데이터 양
while (true)
{
// parent 배열의 모든 값들을 -1로 초기화 합니다.
fill(parent, parent + MAX, -1);
queue<int> q;
q.push(start);
// 데이터를 흘려보낼 경로를 탐색합니다.
while (!q.empty())
{
int curr = q.front();
q.pop();
for (size_t i = 0; i < v[curr].size(); i++)
{
int next = v[curr][i];
// 흘려보낼 공간이 남아있고 이미 선택된 경로가 아니라면
if (limit[curr][next] > flow[curr][next] && parent[next] == -1)
{
// 큐에 삽입후 부모 노드 설정
q.push(next);
parent[next] = curr;
}
}
}
// parent[end]가 -1이라는 것은 parent배열 초기화 이후
// 새로운 경로를 찾지 못했다는 의미 즉 검색이 끝났다는 것을 의미함
if (parent[end] == -1)
return result;
// 최소 유량 찾기
int min = 100000;
for (int i = end; i != start; i = parent[i])
{
// 현재 흘려 보낼 수 있는 양을 구함
// end로 가는 각각의 간선에서 [ 6 ] - [ 4 ] - [ 9 ] 의 유량을 가지고 있다면
// 당연하게도 4만큼의 데이터만 흘려 보낼 수 있음
int c = limit[parent[i]][i] - flow[parent[i]][i];
if (min > c) min = c;
}
// 현재 흐르고있는 데이터를 체크해줌
for (int i = end; i != start; i = parent[i])
{
flow[parent[i]][i] += min;
flow[i][parent[i]] -= min;
}
result += min;
}
}'프로그래밍 > 자료구조와 알고리즘' 카테고리의 다른 글
| 강한 결합 요소(SCC - Strongly Connected Component) (0) | 2023.01.25 |
|---|---|
| 라빈 카프 알고리즘 (0) | 2023.01.18 |
| 위상 정렬 알고리즘 (0) | 2023.01.09 |
| 에라토스테네스의 체 (0) | 2023.01.05 |
| KMP 알고리즘 (1) | 2023.01.03 |