반응형
위상 정렬 알고리즘
- 순환이 없는 방향 그래프에서의 노드들을 순서대로 나열해주는 알고리즘
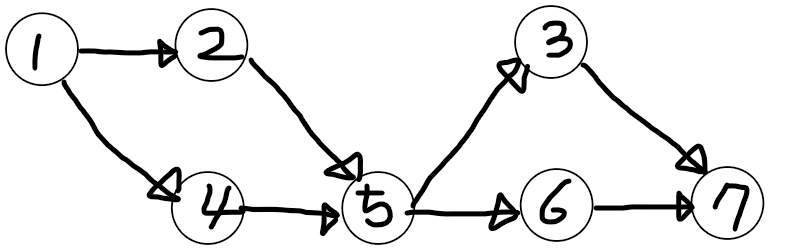
우선 위의 그래프를 위상 정렬 알고리즘을 통해 정렬을 하면
1 - 2 - 4 - 5 - 3 - 6 - 7 이 나옴
정렬 과정

진입 차수가 없는 1번 노드가 가장 먼저 정렬되고
1번 노드에서부터 연결된 노드들의 진입 차수를 1씩 감소 시킴

진입 차수가 없는 노드인 2, 4가 정렬이 되고
2, 4번 노드에서부터 연결된 5번 노드의 진입 차수를 1씩 총 2 감소시킴

진입 차수가 없는 노드인 5번 노드가 정렬이 되고
5번 노드에서부터 연결된 노드인 3, 6번 노드의 진입 차수를 1씩 감소 시킴

진입 차수가 0이된 3, 6번 노드가 이어서 정렬이 완료가 되고
3, 6번 노드에서부터 연결된 7번 노드의 진입 차수를 1씩 총 2감소 시킴

진입 차수가 0이 된 7번 노드가 정렬이 되고
정렬을 종료함
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
vector<vector<int>> v;
vector<int> inDegree;
void TopologySort()
{
queue<int> q;
vector<int> result;
for (int i = 1; i < inDegree.size(); i++)
if (inDegree[i] == 0) q.push(i);
while (!q.empty())
{
int a = q.front();
result.push_back(a);
q.pop();
for (int j = 0; j < v[a].size(); j++)
{
int b = v[a][j];
if (--inDegree[b] == 0)
{
q.push(b);
}
}
}
for (int i = 0; i < result.size(); i++)
cout << result[i] << " ";
}
int main()
{
int N = 7;
v.resize(N + 1);
inDegree.resize(N + 1);
v[1].push_back(2);
inDegree[2]++;
v[1].push_back(4);
inDegree[4]++;
v[2].push_back(5);
inDegree[5]++;
v[4].push_back(5);
inDegree[5]++;
v[5].push_back(3);
inDegree[3]++;
v[5].push_back(6);
inDegree[6]++;
v[3].push_back(7);
inDegree[7]++;
v[6].push_back(7);
inDegree[7]++;
TopologySort();
return 0;
}반응형
LIST
'프로그래밍 > 자료구조와 알고리즘' 카테고리의 다른 글
| 라빈 카프 알고리즘 (0) | 2023.01.18 |
|---|---|
| 네트워크 플로우 알고리즘 (0) | 2023.01.12 |
| 에라토스테네스의 체 (0) | 2023.01.05 |
| KMP 알고리즘 (1) | 2023.01.03 |
| 다익스트라(Dijkstra) - O(E * logE) (0) | 2022.12.21 |