Matrix Layer Rotation | HackerRank
Rotate the matrix R times and print the resultant matrix.
www.hackerrank.com
행렬과 왼쪽으로 회전하는 횟수 r을 입력 받을 때, 회전된 모습을 출력 하는 문제입니다.
풀이 방법
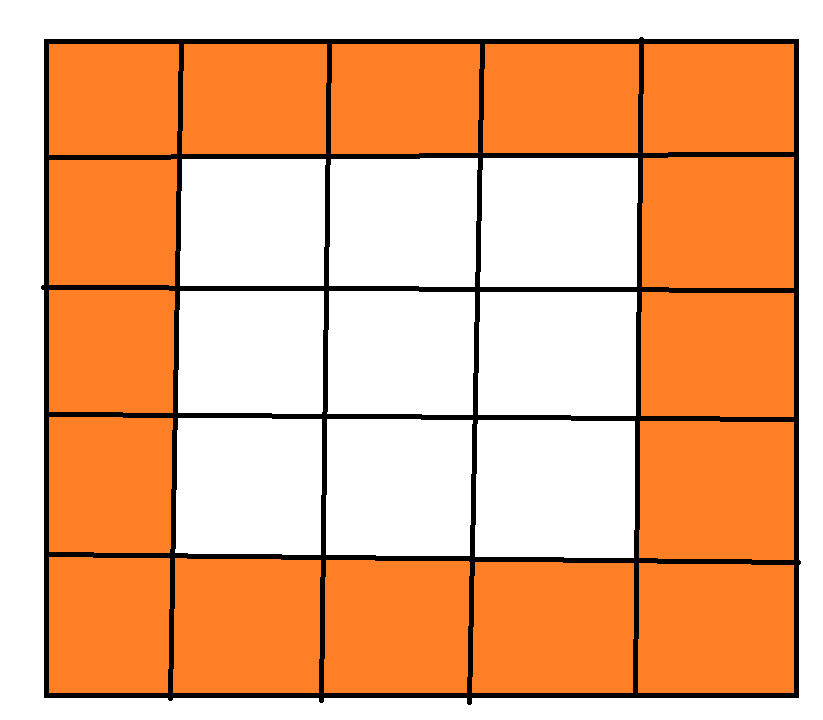
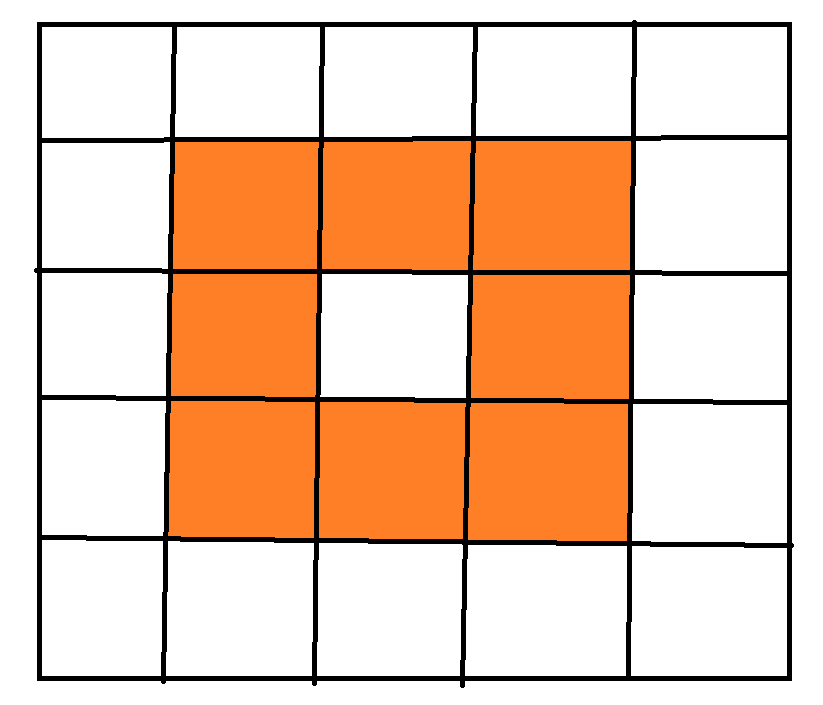
회전하는 각 테두리를 각각의 deque에 넣어주었습니다.
그와 동시에 deque를 행렬로 옮기기 쉽도록 deque 배열이 가지고 있는 각 index의 행렬 좌표를 따로 저장해두었습니다.
vector<deque<int>> dqs;
vector<vector<pair<int, int>>> poss;
dequq에서 회전을 마친 이후 아래 코드를 통해 간단하게 행렬로 옮길 수 있습니다.
for (int i = 0; i < int(dqs.size()); i++)
{
for (int j = 0; j < int(dqs[i].size()); j++)
{
auto [y, x] = poss[i][j];
matrix[y][x] = dqs[i][j];
}
}
회전하는 각 테두리의 정보를 옮길 때에는 테두리의 꼭지점 정보를 이용했습니다.
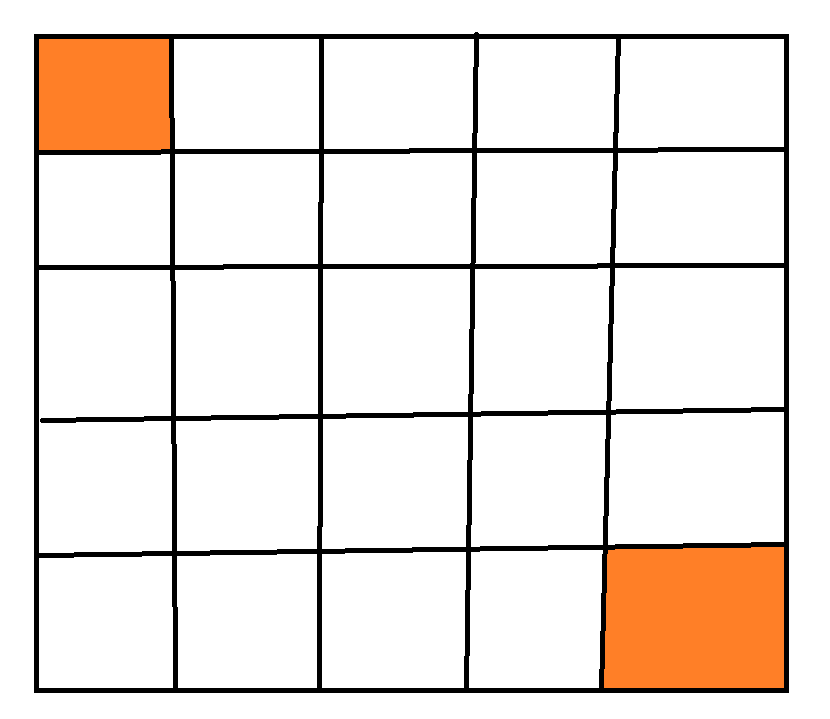
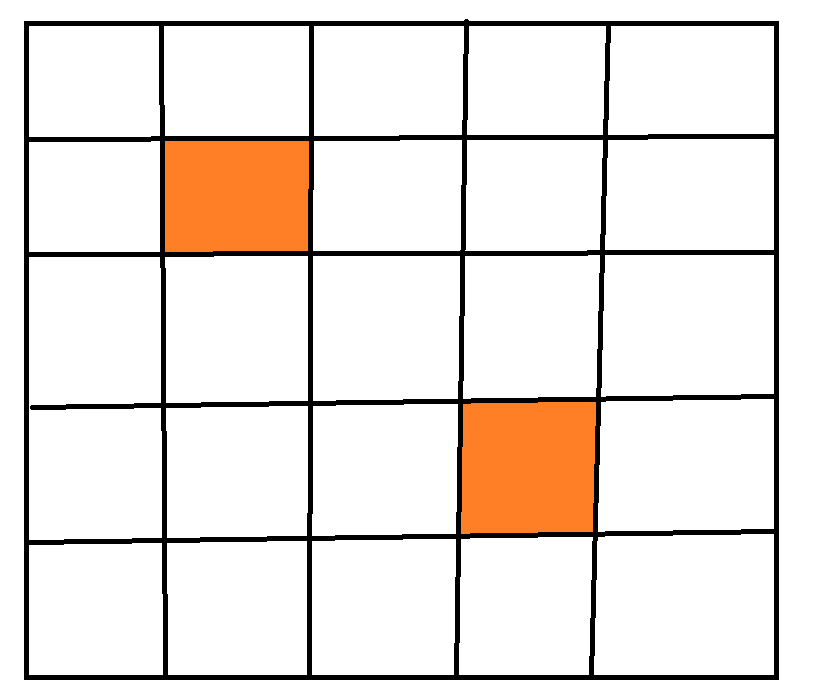
각 테두리의 꼭지점 위치 값을 왼쪽 위는 [y1, x1] 이라 칭하고, 오른쪽 아래는 [y2, x2]라고 칭할 때,
[y1, x1] ~ [y1, x2]을 먼저 저장 이후에 (위쪽)
[y1+1, x2] ~ [y2-1, x2]를 저장, (오른쪽)
[y2, x2] ~ [y2, x1]을 저장, (아래)
[y2-1, x1] ~ [y1+1, x1] 순서로 저장 했습니다.
이후 [y1, x1]에는 각 1씩 더해주고 [y2, x2]에는 각 1씩 빼주어 위 과정을 반복하였습니다.
r은 최대 1,000,000,000이기 때문에 이것을 단축 시킬 방법이 필요합니다.
행렬은 한바퀴를 회전 하면 재자리로 돌아옵니다. 즉, 테두리의 길이가 30일때, r이 30이라면 계산이 필요하지 않으며, r이 100일때에는 100 % 30 (10) 만 회전하면 된다는 뜻입니다.
코드로 표현하자면 r % dps[i].size() 만큼만 데이터를 옮기면 되겠습니다.
정답 코드
void matrixRotation(vector<vector<int>> matrix, int r) {
int M = matrix.size();
int N = matrix[0].size();
pair<int, int> start = {0, 0};
pair<int, int> end = {M-1, N-1};
// 테두리의 수를 저장하는 deque, 위치 값을 저장하는 vector
vector<deque<int>> dqs;
vector<vector<pair<int, int>>> poss;
while (start.first < end.first && start.second < end.second)
{
deque<int> d;
vector<pair<int, int>> pos;
// 테두리의 위쪽 저장
for (int i = start.second; i <= end.second; i++){
d.push_back(matrix[start.first][i]);
pos.push_back({start.first, i});
}
// 테두리의 오른쪽 저장
for (int i = start.first+1; i < end.first; i++){
d.push_back(matrix[i][end.second]);
pos.push_back({i, end.second});
}
// 테두리의 아래쪽 저장
for (int i = end.second; i >= start.second; i--){
d.push_back(matrix[end.first][i]);
pos.push_back({end.first, i});
}
// 테두리의 왼쪽 저장
for (int i = end.first-1; i > start.first; i--){
d.push_back(matrix[i][start.second]);
pos.push_back({i, start.second});
}
dqs.push_back(d);
poss.push_back(pos);
start.first++;
start.second++;
end.first--;
end.second--;
}
// 회전 시키기
for (int i = 0; i < int(dqs.size()); i++)
{
for (int j = 0; j < (r % int(dqs[i].size())); j++)
{
auto a = dqs[i].front();
dqs[i].pop_front();
dqs[i].push_back(a);
}
}
// 데이터를 행렬로 옮기기
for (int i = 0; i < int(dqs.size()); i++)
{
for (int j = 0; j < int(dqs[i].size()); j++)
{
auto [y, x] = poss[i][j];
matrix[y][x] = dqs[i][j];
}
}
// 출력하기
for (const auto& row : matrix) {
for (int val : row) {
cout << val << " ";
}
cout << endl;
}
}
'알고리즘 문제 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 자동차 평균 대여 기간 구하기 [Lv. 2] (MySQL) (0) | 2024.10.28 |
|---|---|
| 프로그래머스 분기별 분화된 대장균의 개체 수 구하기 [Lv. 2] (MySQL) (0) | 2024.10.28 |
| 프로그래머스 석유 시츄 [Lv. 2] (C++) (0) | 2024.10.25 |
| 프로그래머스 동영상 재생기 [Lv. 1] (C++) (0) | 2024.10.25 |
| 프로그래머스 붕대 감기 [Lv. 1] (C++) (0) | 2024.10.25 |