반응형
다익스트라 알고리즘은 최단 경로 탐색 알고리즘임
하나의 시작점에서부터 모든 정점까지의 최단 경로를 탐색함
다익스트라 알고리즘의 핵심
- 목표로하는 노드의 최소비용 = min(내 위치까지의 비용 + 내 위치에서 목표 노드로의 비용, 현재까지 알려진 목표 노드의 최소비용)
예제 그래프
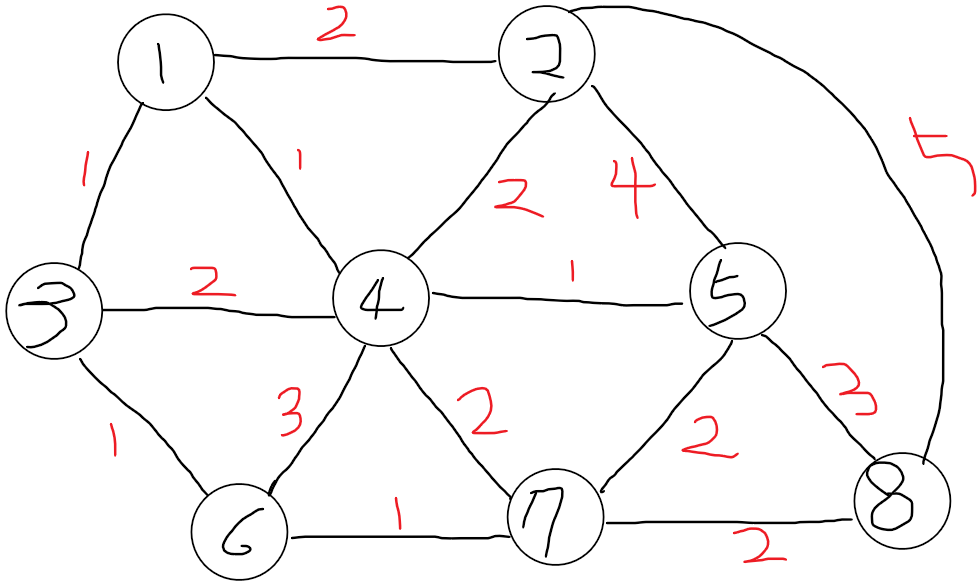
int MAX = 1000000000;
int cost[8]; // 각 정점으로의 최소비용을 담을 예정
int w[8][8]
{
{0, 2, 1, 1, MAX, MAX, MAX, MAX},
{2, 0, MAX, 2, 4, MAX, MAX, 5},
{1, MAX, 0, 2, MAX, 1, MAX, MAX},
{1, 2, 2, 0, 1, 3, 2, MAX},
{MAX, 4, MAX, 1, 0, MAX, 2, 3},
{MAX, MAX, 1, 3, MAX, 0, 1, MAX},
{MAX, MAX, MAX, 2, 2, 1, 0, 2},
{MAX, 5, MAX, MAX, 3, MAX, 2, 0}
};코드로는 이렇게 표현이 가능
위에서 말한 다익스트라 알고리즘의 핵심을 생각해보면
이처럼 간단하게 코딩해볼 수 있음
void dijkstra(int start)
{
for (int i = 0; i < N; i++)
cost[i] = g[start][i]; // 시작 노드에서부터 모든 정점으로의 비용을 등록
for (int current = 0; current < N; current++)
{
for (int dest = 0; dest < N; dest++)
{
if (cost[dest] > cost[current] + g[current][dest])
cost[dest] = cost[current] + g[current][dest];
} // 목표로하는 노드의 최소비용 = 현재 위치까지의 최소비용 + 현재 위치에서 목표 노드로의 비용
}
}int main()
{
dijkstra(0); // 0 2 1 1 2 2 3 5
dijkstra(1); // 2 0 3 2 3 4 4 5
for (int i = 0; i < N; i++)
cout << cost[i] << " ";
return 0;
}
다익스트라를 N * logN으로 구현하고 싶다면..
다익스트라(Dijkstra) - O(E * logE)
다익스트라 문제를 E* logE로 해결하기 위해서는 정점(V)에 초점을 두는 것이 아니라 간선(E)에 초점을 두고 코딩을 해야함 int MAX = 1000000000; int cost[8]; // 각 정점으로의 최소비용을 담을 예정 vector v
flrjtwjrjt.tistory.com
반응형
LIST
'프로그래밍 > 자료구조와 알고리즘' 카테고리의 다른 글
| KMP 알고리즘 (1) | 2023.01.03 |
|---|---|
| 다익스트라(Dijkstra) - O(E * logE) (0) | 2022.12.21 |
| 크루스칼 알고리즘과 유니온 파인드 (0) | 2022.11.28 |
| 퀵정렬 (0) | 2022.11.27 |
| stack (0) | 2022.11.13 |